DFS是一种深度优先遍历的算法,可以理解为一条道走到头,然后回来从另一条路再走到头,用递归实现
BFS是一种广度优先遍历的算法,当遇到岔路时将所有节点存到队列中,然后依次找下一个相连的节点,用队列实现
DFS
排列数字
给定一个整数 n,将数字 1∼n 排成一排,将会有很多种排列方法。
现在,请你按照字典序将所有的排列方法输出。
输入格式
共一行,包含一个整数 n。
输出格式
按字典序输出所有排列方案,每个方案占一行。
数据范围
1≤n≤7
输入样例:
3
输出样例:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1#include<bits/stdc++.h>
using namespace std;
int n;
int a[10],ans,b[10];
void dfs(int u){
a[ans++]=u;
if(ans==n){
for(int i=0;i<n;i++){
cout<<a[i]<<" ";
}
cout<<endl;
return;
}
for(int i=1;i<=n;i++){
if(!b[i]){
b[i]=1;
dfs(i);
b[i]=0;
ans--;
}
}
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
if(!b[i]){
b[i]=1;
dfs(i);
b[i]=0;
ans--;
}
}
return 0;
}n-皇后问题
n−n−皇后问题是指将 nn 个皇后放在 n×nn×n 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
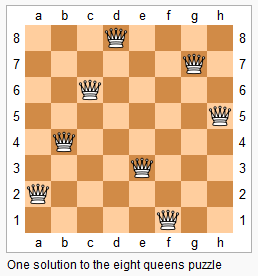
现在给定整数 nn,请你输出所有的满足条件的棋子摆法。
输入格式
共一行,包含整数 n。
输出格式
每个解决方案占 n 行,每行输出一个长度为 n 的字符串,用来表示完整的棋盘状态。
其中 . 表示某一个位置的方格状态为空,Q 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
注意:行末不能有多余空格。
输出方案的顺序任意,只要不重复且没有遗漏即可。
数据范围
1≤n≤9
输入样例:
4输出样例:
.Q..
...Q
Q...
..Q.
..Q.
Q...
...Q
.Q..#include<bits/stdc++.h>
using namespace std;
int l[10],zx[20],yx[20];
char a[10][10];
int n;
void dfs(int r){
if(r==n){
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cout<<a[i][j];
}
cout<<endl;
}
cout<<endl;
return;
}
for(int i=0;i<n;i++){
if(!l[i]&&!zx[r-i+n]&&!yx[r+i]){
a[r][i]='Q';
l[i]=1;
zx[r-i+n]=1;
yx[r+i]=1;
dfs(r+1);
a[r][i]='.';
l[i]=0;
zx[r-i+n]=0;
yx[r+i]=0;
}
}
}
int main(){
cin>>n;
memset(a,'.',sizeof a);
dfs(0);
return 0;
}树的重心
给定一颗树,树中包含 nn 个结点(编号 1∼n)和 n−1 条无向边。
请你找到树的重心,并输出将重心删除后,剩余各个连通块中点数的最大值。
重心定义:重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中点数的最大值最小,那么这个节点被称为树的重心。
输入格式
第一行包含整数 n,表示树的结点数。
接下来 n−1 行,每行包含两个整数 a 和 b,表示点 a 和点 b 之间存在一条边。
输出格式
输出一个整数 m,表示将重心删除后,剩余各个连通块中点数的最大值。
数据范围
1≤n≤105
输入样例
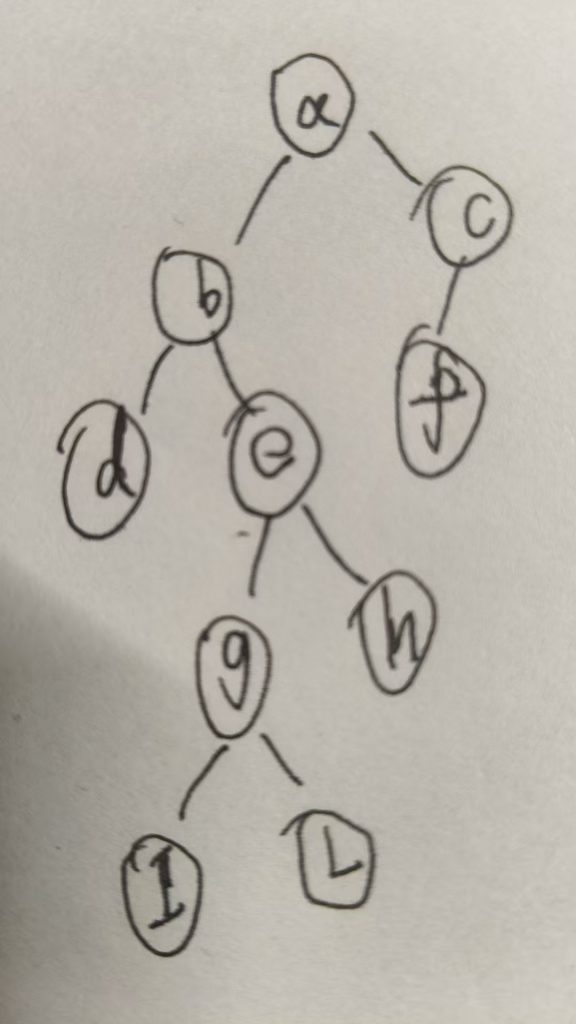
9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6
输出样例:
4/*先假设每个点都是重心,然后判断将这个点删除后剩下的连通块中节点数的最大值,找出这些最大值中的最小值就是真正重心删除后剩余连通块中点数的*/
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
int e[N*2],ne[N*2],h[N],idx,ans=1e9+10,n;
int st[N];
void add(int a,int b){
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
}
int dfs(int u){
st[u]=1;
int sum=1,res=0;
for(int i=h[u];i!=-1;i=ne[i]){
int j = e[i];
if(!st[j]){
int s = dfs(j);
res = max(res,s);//表示这个节点的子树的最大点数
sum += s;//表示加上这个根节点的子树的点数
}
}
res = max(res,n-sum);
//更新为去掉包括这个节点的子树的点数的最大值(比如图中的节点e,把以e为根节点的子树去掉,剩下的节点数)
ans = min(ans,res);//记录所有结果中的最小值
return sum;
}
int main(){
memset(h,-1,sizeof h);
cin>>n;
for(int i=1;i<n;i++){
int a,b;
cin>>a>>b;
add(a,b),add(b,a);
}
dfs(1);
cout<<ans<<endl;
return 0;
}
BFS
走迷宫
给定一个 n×mn×m 的二维整数数组,用来表示一个迷宫,数组中只包含 00 或 11,其中 00 表示可以走的路,11 表示不可通过的墙壁。
最初,有一个人位于左上角 (1,1)(1,1) 处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
请问,该人从左上角移动至右下角 (n,m)(n,m) 处,至少需要移动多少次。
数据保证 (1,1)(1,1) 处和 (n,m)(n,m) 处的数字为 00,且一定至少存在一条通路。
输入格式
第一行包含两个整数 nn 和 mm。
接下来 nn 行,每行包含 mm 个整数(00 或 11),表示完整的二维数组迷宫。
输出格式
输出一个整数,表示从左上角移动至右下角的最少移动次数。
数据范围
1≤n,m≤100
输入样例:
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
输出样例:
8#include<bits/stdc++.h>
using namespace std;
int hx[4]={0,0,1,-1};
int hy[4]={1,-1,0,0};
int con[110][110],a[110][110],b[110][110],n,m;
queue< pair<int,int> >qe;
void bfs(){
qe.push({0,0});
while(!qe.empty()){
auto t = qe.front();
qe.pop();
int x=t.first;
int y=t.second;
for(int i=0;i<4;i++){
int xx=x+hx[i],yy=y+hy[i];
if(xx>=0&&xx<n&&yy>=0&&yy<m){
if(b[xx][yy]==0&&con[xx][yy]==0){
qe.push({xx,yy});
b[xx][yy]=1;
a[xx][yy]=a[x][y]+1;
}
}
}
}
}
int main(){
cin>>n>>m;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
cin>>con[i][j];
}
}
bfs();
cout<<a[n-1][m-1];
return 0;
}八数码
在一个 3×3 的网格中,1∼8 这 8 个数字和一个 x 恰好不重不漏地分布在这 3×3 的网格中。
例如:
1 2 3
x 4 6
7 5 8
在游戏过程中,可以把 x 与其上、下、左、右四个方向之一的数字交换(如果存在)。
我们的目的是通过交换,使得网格变为如下排列(称为正确排列):
1 2 3
4 5 6
7 8 x
例如,示例中图形就可以通过让 x 先后与右、下、右三个方向的数字交换成功得到正确排列。
交换过程如下:
1 2 3 1 2 3 1 2 3 1 2 3
x 4 6 4 x 6 4 5 6 4 5 6
7 5 8 7 5 8 7 x 8 7 8 x
现在,给你一个初始网格,请你求出得到正确排列至少需要进行多少次交换。
输入格式
输入占一行,将 3×33×3 的初始网格描绘出来。
例如,如果初始网格如下所示:
1 2 3
x 4 6
7 5 8
则输入为:1 2 3 x 4 6 7 5 8
输出格式
输出占一行,包含一个整数,表示最少交换次数。
如果不存在解决方案,则输出 −1。
输入样例:
2 3 4 1 5 x 7 6 8输出样例
19#include<bits/stdc++.h>
using namespace std;
int dx[]={1,-1,0,0};
int dy[]={0,0,1,-1};
int bfs(string s){
string end = "12345678x";
queue < string > qe;
unordered_map < string , int > mp;
qe.push(s);
mp[s]=0;
while(qe.size()){
auto t = qe.front();
qe.pop();
int sum = mp[t];
if(t == end)return sum;
int k = t.find('x');
int x = k/3,y = k%3;
for(int i=0;i<4;i++){
int xx = x + dx[i],yy = y + dy[i];
if(xx>=0&&xx<3&&yy>=0&&yy<3){
swap(t[k],t[xx*3+yy]);
if(!mp.count(t)){
mp[t] = sum+1;
qe.push(t);
}
swap(t[k],t[xx*3+yy]);
}
}
}
return -1;
}
int main(){
string s;
for(int i=0;i<9;i++){
string c;
cin>>c;
s+=c;
}
cout<<bfs(s)<<endl;
return 0;
}用字符串来存每一步的状态,其中 x = 下标/3,y = 下标%3,然后定义应该map数组存走过的状态,其中unordered_map 与 map 的区别是 map 存储和查询的时间复杂度都是Ologn,unordered_map 存储On,查询O1,在有大量查询操作时unordered_map更有优势
图中点的层次
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环。
所有边的长度都是 1,点的编号为 1∼n。
请你求出 1 号点到 n 号点的最短距离,如果从 1 号点无法走到 n 号点,输出 −1。
输入格式
第一行包含两个整数 nn 和 mm。
接下来 m 行,每行包含两个整数 a 和 b,表示存在一条从 a 走到 b 的长度为 1 的边。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
数据范围
1≤n,m≤105
输入样例:
4 5
1 2
2 3
3 4
1 3
1 4
输出样例:
1#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
int e[N*2],ne[N*2],h[N],idx,n,m;
int st[N],num[N];
queue<int>qe;
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void bfs(int u){
st[u]=1;
qe.push(u);
while(!qe.empty()){
int t = qe.front();
qe.pop();
for(int i=h[t];i!=-1;i=ne[i]){
int j = e[i];
if(!st[j]){
qe.push(j);
st[j]=1;
num[j]=num[t]+1;
}else{
num[j]=min(num[j],num[t]+1);
}
}
}
}
int main(){
memset(h,-1,sizeof h);
memset(num,-1,sizeof num);
num[1]=0;
cin>>n>>m;
while(m--){
int a, b;
cin>>a>>b;
add(a,b);
}
bfs(1);
cout<<num[n]<<endl;
return 0;
}